Democrats lead in House generic ballot polls by 2.3 points

How our new generic ballot average works, and what a 2-3 point Dem. win would look like in Congress

Today, Strength In Numbers is launching our long-awaited average of congressional generic ballot polls! The initial results show a national electoral environment leaning slightly toward the Democrats, a small but significant shift to the left since the 2024 election.

If the 2026 midterm elections were held today (and polls were exactly correct), our average finds 45.3% of voters would cast ballots for Democratic candidates for the U.S. House of Representatives, while 43% would vote for Republicans. That makes for a +2.3-point margin for the Democratic Party, a lead that is outside the margin of error of our average.

---

---

This average will be updated at least once daily and is available on the Strength In Numbers data portal. The polls being used in this average are available here.

The methodology for this average is detailed below.

---

---

Democrats ahead of normal midterm position, lag 2018

At 43%, support for Republicans is down nearly 5 percentage points from the start of the year. Democrats have increased their support by two points, from 43% on President Donald Trump's first day in office to just over 45% now.

Currently, Democrats lag behind their position at this point in the 2018 and 2006 midterm elections. But they are outperforming where the average “out-party” — the major party that is not in control of the White House — has been at this point in the cycle over the last 5 midterms.

From 2006 to 2022, the out-party was, on average, tied in the generic ballot in late July of the year before the midterm. Then, on average, that party gained 6 points in generic ballot polls over the following 16 months:

• 2022: Out-party: -4 (won by +3)

• 2018: Out-party: +6 (won by +8)

• 2014: Out-party: -3 (won by +6)

• 2010: Out-party: -4 (won by +7)

• 2006: Out-party: +5 (won by +8)

• Average: Out-party: +0 (won by 6)

• Today: Out-party: +2.3

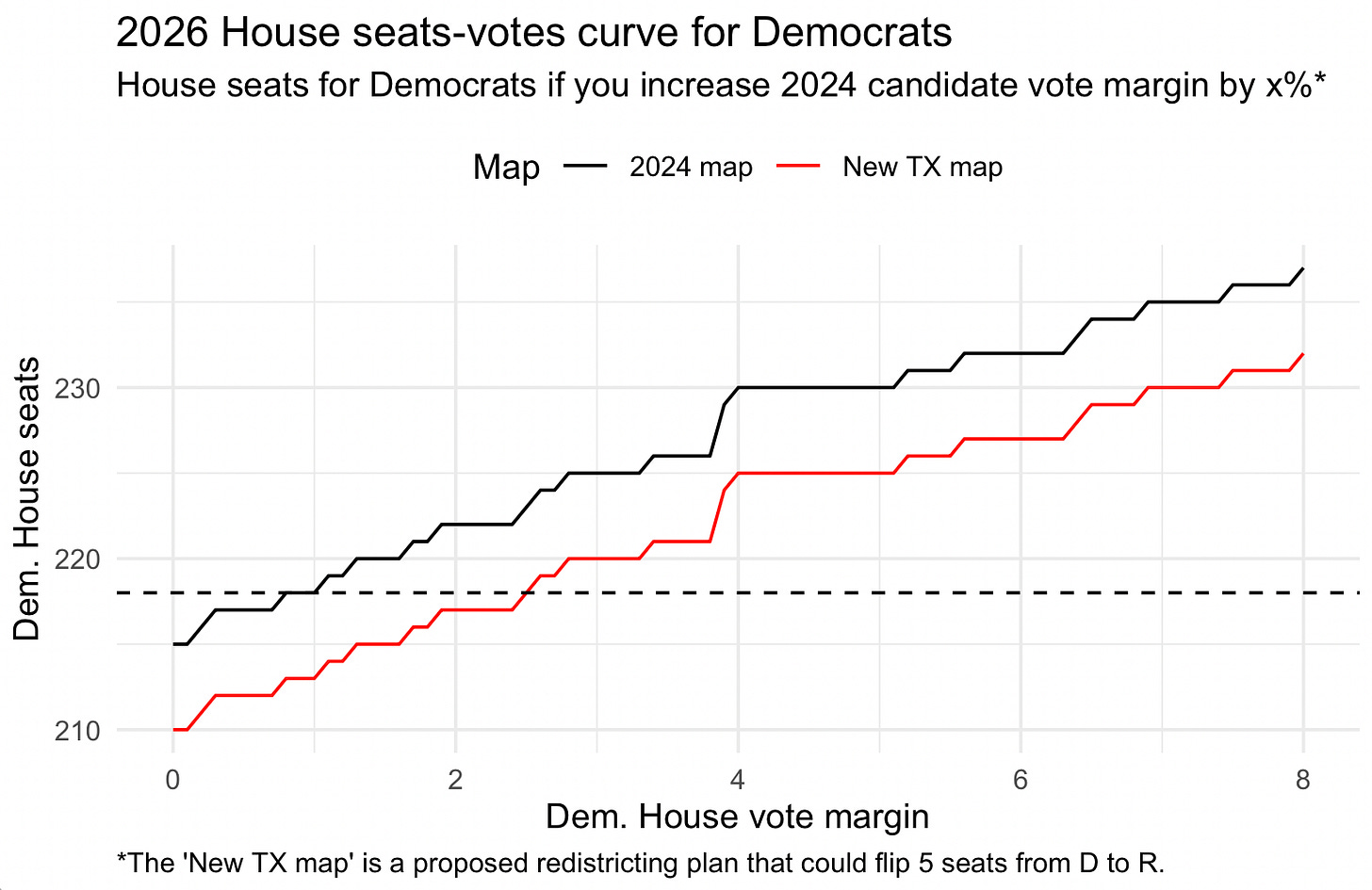
To get a rough idea of what Democrats need to win the U.S. House next year, I have simulated several thousand alternative 2024 election outcomes based on two variables: (a) how many seats Republicans in Texas manage to gerrymander away from Democrats, and (b) the size of the Democratic share of the national House popular vote next November. Under the current map, a 2.5-point win translates to a 5-point swing since last November, and Democrats winning 222 House seats. At 8 points — the size of the 2018 "blue wave", Democrats would win 237 seats.

Under current lines, Democrats need to win the House popular vote by roughly 1.5 points to be favored to win the majority of seats. If Texas Republicans can swing 5 seats away from Democrats, as their current plan likely does, Democrats will need to win the House popular vote by roughly 2.5-3 points to win the majority of seats.

In the Senate, a modest Democratic margin of circa ~3 points would likely not be enough for Democrats to regain control of the chamber. The party needs to win two GOP-held seats in either Florida, Iowa or Texas, in addition to picking up North Carolina and Maine, in order to win the 51 seats necessary to override a tie-breaker from Vice President JD Vance. But Florida, Iowa and Texas each usually leans to the GOP by double digits in federal elections. A national swing of 5-6 points left is unlikely to be large enough to carry even a popular, well-matched candidate to victory in those Likely Republican seats (though it is not impossible).

Two caveats: First, and obviously, the election will not be held today; things can and will change over the next 16 months. And second, the simulation exercise above does not take candidate quality, demographic shifts, or other redistricting changes into account — it is an exercise in projecting average changes given different vote shares. It is a rough guide to the future, not a certainty.

Our average should not be treated as a forecast of the outcome in November, but a tool to track the political environment, according to polls, as they exist today, at this snapshot in time. If the Democrats meet or grow their current level of support, they’ll probably win the House majority next year. Let’s watch the data and update our beliefs over time.

---

Methodology

Our method for averaging generic ballot polls draws on existing journalistic approaches to aggregation as well as academic literature on Bayesian time-series models. Our average adjusts polls for recency, pollster quality and statistical bias, sample size, the population a pollster targets, and the methodological “modes” a pollster used to sample and interview voters.

We model our approach on Elliott's past work for The Economist, Professor Simon Jackman's pioneering work "pooling the polls", and existing poll-averages in the Bayesian programming language Stan. A primitive version of this methodology was released publicly by Elliott for 538 in 2025. We built on these approaches from scratch, and now add to the literature on Bayesian aggregation by regularizing daily changes in opinion.

Which polls we include

For the most part, our average uses every publicly available poll that (a) releases enough data (poll sponsor, topline) about its results and meets our standards for methodology and pollster ethics. We then filter this dataset based on the following questions:

1. Which version should we use? Whenever a pollster releases multiple versions of a survey — say, an estimate of Trump's approval rating among both all adults and just registered voters — we prefer the version that samples likely voters, then registered voters, then all adults.

2. Is this a tracking poll? Some pollsters release daily results of surveys that may overlap with each other. We account for this potential overlap in these "tracking" polls by running through our database every day and dynamically removing polls that have field dates that overlap with each other until none are overlapping. We always hold on to the most recent poll.

3. Do we know the sample size? Some pollsters do not report sample sizes with their surveys. We usually combat this by emailing or calling the pollster, but sometimes, that data remains elusive. For these polls, we first assume that a missing sample size is equal to the median sample size of other polls from that same pollster. Then, we impute the sample size using the median sample size of all other polls in question. As a default, we cap sample sizes at 5,000 to minimize the influence of large-N surveys. Then, we use a method called winsorizing to limit extreme values.

---

Support data-driven journalism!

Become a paying member of Strength In Numbers today and get exclusive posts, early access to data, and more.

Your support helps fund polling trackers, original polls, deep analysis, and data-driven journalism that cuts through the noise of today’s media landscape. Support our site and tell the world that when it comes to the news and democracy, there is strength in numbers.

---

How we weight polls

After we have our polling data, we compute three weights for each survey that control how much influence it has in our average, based on the following factors:

1. Sample size. We weight polls using a function that involves the square root of its sample size. We want to account for the fact that additional interviews have diminishing returns after a certain point. The statistical formula for a poll's margin of error — a number that pollsters (usually) release that tells us how much their poll could be off due to random sampling error alone — uses a square-root function, so our weighting does, too.

2. Multiple polls in a short window. We want to avoid a situation where a single pollster floods an average with its data, overwhelming the signal from other pollsters. To do that, we decrease the weight of individual surveys from pollsters that release multiple polls in a short period. If a pollster releases multiple polls within a 14-day window, those polls each receive a reduced weight equal to the square root of 1 over the number of polls inside that window. That means if a pollster releases two polls in two weeks, each would receive a weight of 0.71 (the square root of 0.5). If it releases three polls, each would receive a weight of 0.57 (the square root of 0.33).

3. Pollster rating. Polls are weighted by the latest release of 538's pollster ratings, which we archived from the site's GitHub page. To calculate the weight we give to a poll based on its pollster's 538 rating, we first divide its rating by 3 (the maximum possible score) and take the square root of the resulting number. For example, a pollster that we give 0.5 stars out of 3 gets 41% of the weight that a 3-star poll gets.

These three weights are all multiplied together into a cumulative weight for our aggregation model.

How we average polls together

Once we have all our polls and weights, it is time to average them together.¹

The model is similar to the one I use for averaging Trump approval polls, and derivations of it have been used to model approval ratings of government leaders in the United Kingdom and for elections in Australia. Oversimplifying a bit, you can think of this "polling average" as one giant model that is trying to predict the results of polls we collect based on (1) the overall state of public opinion on any given day and (2) various factors that could have influenced the result of a particular poll, plus (3) random noise due to sampling and non-sampling error. These factors are:

1. The polling firm that conducted the poll. Some polls systematically over- or under-shoot support for certain candidates, which we call "house effects" for each pollster. We measure the house effect for each firm using something called a random-effects model, which essentially captures how much more pro- or anti-Democratic/Republican each pollster is on average, relative to all the other polls in our dataset. We then subtract that number from the results for that pollster's polls to ensure they're not biasing our averages.

2. The mode used to conduct the poll. Different groups of people answer polls in different ways. Young people are likelier to be online, for instance, and phone polls reach older, whiter voters more readily. Similar to the house effects adjustment above, we apply a mode-effects adjustment to correct for residual methodology-related biases before we aggregate those surveys.

3. Whether the poll sampled likely voters, registered voters, or all adults. Historically, polls of likely voters have been more accurate in anticipating the House popular vote than polls of registered voters or all adults. So we also have our model look for any systematic differences between likely-voter, registered-voter, and all-adult polls and subtract those differences from the latter two types of polls. This gives us an average that is more closely comparable to historical trends. The population adjustment is currently turned off due to a low supply of likely-voter polls this far before the midterms. It will gradually ramp up as Nov. 2026 approaches.

4. Whether the poll was conducted by a campaign or other partisan organization. We apply a partisanship adjustment to account for predictable pro-D/R effects of a poll being conducted or sponsored by a partisan organization. For example, if a poll sponsored by a Republican-friendly organization gives a result that is more favorable to Republican House candidates than another poll, we subtract some of the difference. The size of the partisan adjustment is usually about 2.4 percentage points, but our model is constantly adjusting that number to match the data.

Finally, our prediction for a given poll also accounts for the value of the polling average on the day it was conducted. That's because if overall support for the Democrats is 50 percent, we should expect polls from that day to reveal higher support than if the Democrats were at say, 45%. This also means the model implicitly puts less weight on polls that look like huge outliers, after adjusting for all the factors above.

That brings up the question of how exactly the average is being calculated.

A random walk down Constitution Ave.

We use a modified random walk to calculate the average support for Democrats and Republicans over time. In essence, we tell our computers that support for each party in national polls should start at some point on Day 1 and move by some amount on average each subsequent day. Support for the Democrats might move by 0.1 points on Day 2, -0.2 points on Day 3, 0.4 points on Day 4, 0 points on Day 5, and so on and so on. Every time we run our model, it determines the likeliest values of these daily changes in Dem/Rep vote share while adjusting polls for all the factors mentioned above. We can extract those daily values and add them to the starting value for the Democrats or Republicans at the beginning of our average.

Now, two notes. First, after doing a lot of research into elections, and especially using random walks for public opinion, I generally no longer use normal distributions for daily changes in opinion (what is usually meant by “random walk”). This is because daily changes in opinion are not normally distributed. Instead, most days go by without much change in opinion, but there are periods of disjunction where larger-than-predicted jumps occur. Normal distributions also put a lot more mass in the hips of the curve, overestimating shifts in opinion at the 60th-80th percentile range. To better capture the tendency for most days to show little to no movement, and for some days to show a lot, you want a fat-tailed distribution "doing the walking" (so to speak). In our model, daily changes in opinion are drawn from a double-exponential distribution.

As for the second wrinkle: We actually run not one but three different versions of our average to account for the chance that daily volatility in public opinion changes over time. For every day of the midterm cycle, we calculate one estimate of Dem/Rep support by running our model with all polls from the last 180 days, one with all polls from the last 90 days, and one with all polls from the last 30 days. Then, we take the final values for those three models and average them together. This helps our aggregate react to quick changes in opinion while removing noise from periods of stability.

Finally, we do account for additional detectable error in a poll (sometimes called an "outlier adjustment"). This is noise that goes above and beyond the patterns of bias we can account for with the adjustments listed above, or uncertainty caused by the traditional margin of sampling error in a poll. That traditional MOE only captures noise derived from the number of interviews a pollster does: A larger sample size means less variance due to "stochasticity" (random weirdness) in a poll's sample.

But there is also non-sampling error in each poll — a blanket term encompassing any additional noise that could be a result of faulty weights, certain groups not picking up the phone, a bad questionnaire design or really anything else that we haven't added explicit adjustment factors for. Our model measures how much non-sampling error is present across the polls by adding additional error to each poll beyond that which is implied by each poll's sample size via the sum of squares formula. The model decides how large this extra error should be.

How we measure uncertainty

The final thing to do is calculate how much error there might be in our estimates. This error comes from sampling error in the polls themselves, as well as uncertainty about all our model's various adjustments.

Unlike other approaches, our model accounts for uncertainty in the polling average as a direct product of calculating that average, and in a very straightforward way. Imagine we are not calculating support for each party one single time, but thousands of times, where each time we see what his support would be if the data and parameters of our model had different values. For example, what if the latest poll from The New York Times/Siena College had Democrats doing 3 points better, as a poll of 1,000 people would be expected to show about 5% of the time? Or what if the population adjustment were smaller?

Our model answers these questions by simulating thousands of different polling averages each time it runs. That, in turn, lets us show uncertainty intervals directly on the average.²

Conclusion

And that's it! The Strength In Numbers average of generic ballot polls will update regularly as new polls are released, and at least daily. If you spot a poll that we haven't entered after a business day, or have other questions about our methodology, feel free to email our polling inbox at polls@gelliottmorris.com.

1. The most commonly used polling averages for U.S. public opinion have followed one of three approaches:

1. Take a simple moving average of polls released over some number of previous days.

2. Calculate a trendline through the polls using various statistical techniques, such as a polynomial trendline, spline, or Kalman filter.

3. Combine these approaches, putting a certain amount of weight on the moving average and the rest on the fancier trend.

Usually I do the third option. The average-of-averages approach allows you to use predictions from the best parts of a slow-moving exponentially weighted moving average and a fast-moving polynomial trendline, it is computationally efficient to do so, and it's easy to explain this model to the public. It's also relatively trivial to tweak the model if we find something is working incorrectly.

However, this model has some shortcomings too. First, it's a bit of a Frankenstein situation: the model-of-models uses separate models to reduce the weight on polls that are very old or have small sample sizes; then another model to average polls and detect outliers; then another to run new averaging models to detect house effects; and so on and so on.

This chaining of models makes debugging unpredictable, and it's hard to account for uncertainty properly across all the different steps. That's because we potentially generate statistical error every time we move from one model to the next, and would have to run the program thousands of times every time we want to update it! These individual models are also noisier than we'd like, because they do not know about the uncertainty in the other models; You'd end up estimating population effects that are too large if you didn't know about house effects, for example.

Our big Bayesian model solves all these problems by being fast, elegant, and most importantly, comprehensive.

2. People familiar with this method will be quick to point out that, um ackshually, I'm not “simulating” outcomes with different data and parameter values, but drawing samples from the posterior predictive distribution constituted by the MCMC samples estimating the parameters. Yeah, you and I know that, but it's not exactly easy to explain to the average reader. So chill out, Stan stans.